
Exponential Increases of the COVID-19 Virus
Suppose that I am infected with the COVID-19 virus. And at the start of some time period, t0, I am among N0 who are infected. We use the letter N for the number of people infected and t for time in days, and we use the subscript 0 to mean a particular starting time.
Let us assume that there are no restrictions on my movement, or on the movement groups of people playing, attending events, going to the movies, shopping or relaxing on the beach with hundreds of others. So we can go out and be anywhere we want as much as we want.
We are very friendly, and use greetings like in Spain, by shaking hands, hugging and a kissing on the cheek. We do that with everyone we see. We thereby infect these people, as fast as we can move around and as long as there are lots of different uninfected people, so we do not waste our infections on someone we have already infected.
Each of the people we infect are just like us, and they go around and infect other people like we are doing. And each person they infect is just like they are, so they go around infecting yet more other people.
And this just keeps going, on and on.
Because we must move around to infect others, that takes time. But suppose, on the average, each of us can infect another person once every day---just infect one other person a day.
After we infected people for a few days or weeks, we decide to examine what is happening. At some starting time, t0, then, there are N0 -people infected. For example maybe on the 15th day of infections in a community, there were 400 people infected, so t0=15 and N0 = 400.
It is helpful to consider a particular amount of time, like the time between the 15th day, at time t0=15 and the 20th day, say at time tn =20. We would subtract the times and get 20 - 15 = 5. This is called a time interval. For any time interval, we would write it like this, tn - t0.
When the time is t0 there are N0 people infected. When the time is tn , there are Nn people infected.
Because mathematicians are lazy, we make up ways of shortening things we say. A time interval tn - t0 can be shortened by using a Greek symbol for a difference. That symbol is Δ. So tn - t0 can be written as Δt.
Now lets think about the number of infections, ΔN, that would occur within a certain time interval Δt. Within that time interval, the more people who are infected, the more infections they can produce within that interval. The longer the time interval the more people who can be infected. If twice as long, we would expect twice as many infections, if three times as long, three times as many, etc.
We also know that the number of people infected during that time interval Δt would be more if there are already more people infected. With twice as many people already infected, they could infect twice as many others. With three times as many infected, they could infect three times more, etc.
In math, we use something called a proportion. If the ratio of say y to x , y/x, always has the same value, we say that y is proportional to x, and we can write the equation, y = Kx, where K is called the proportionality constant. You have learned gas laws, like Charle's Law, where V/T = K. The Volume is proportional to Absolute Temperature, and V = KT .
For these Covid-19 infections, the number, ΔN infected during a time interval, Δt, is proportional to the number, N0, of people already infected and now infecting others, and it would also be proportional to the amount of time in the interval, Δt. That is,
ΔN/N0Δt = k
The value of the proportionality constant, k, would depend upon how rapidly infections can occur.
Multiplying both sides of that equation by N0Δt, we get the equation,
ΔN = kN0Δt.
Lets keep Δt the same over n intervals, so that if we have an interval t - t0 , there must be n of the small Δt intervals in the larger interval, t - t0. It will be easier to start with a time of zero, so that t0 = 0 and
nΔt = t
and the size of Δt must be,
Δt = t/n
We will look at several of these intervals, ΔN1, ΔN2, ΔN3 ΔN4 , etc.
In the first interval, ΔN1, when n=1 there are
ΔN1 = kN0Δt infections.
At the end of the first interval we must have what we started with plus the amount it increased, or
N1 = N0+ΔN1. But ΔN1 = kN0Δt. So replacing ΔN1 by its value, kN0Δt, we have
N1 = N0 + kN0Δt.
We can now factor out N0.
And we have
N1 = N0(1+ kΔt).
Now lets do the same for the next interval. ΔN2 = kN1Δt, or
N2= N1 + N1kΔt.
Again, we factor out the N1.
And we have,
N2= N1(1 + kΔt).
Since we already found N1 to have the value, N0(1+ kΔt), we can use it to replace the value in the equation for N2. So that we have,
N2=N0(1+kΔt)(1+kΔt).
Using exponents, we can write the factor, (1=kΔt)(1=kΔt) as (1+kΔt)2.
So we have
N2=N0(1+kΔt)2.
Now lets do the same for N3.
N3=N2+N2kΔt.
Factoring out the N2, we have
N3=N2(1+kΔt)
Again we can replace N2 by the value we found for it, getting,
N3=N0(1+kΔt)2(1+kΔt) = N0(1+kΔt)3
If we keep doing this, you can see what will happen to that exponent. For N4, the exponent will be 4. So what will it be when we get to, Nn? Yes, we will then have the equation,
Nn=N0(1+kΔt)n.
But Nn is the number of infections at time t. Since there are n intervals Δt in the total time t, the time t must be t = nΔt, and we can then divide both side by n and get Δt=t/n, We can replace kΔt in our equation by kt/n. So we now have,
N=N0(1+kt/n)n .
We will divide both sides by N0 to get just the quantity (1+kt/n)n with the exponent.
Thus, N/N0=(1+kt/n)n
The quantity in the parentheses has two terms. It is called a binomial. You may remember from elementary algebra how to expand a binomial in what is called the binomial series.
Remember,
(1+a)n = 1 + na + n(n-1)a2/2! + n(n-1)(n-2)a3/3! +…..n(n-1)(n-2)(n-3)a4/4! + ……
Which, for a = kt/n, gives us,
(1+kt/n)n = 1 + n(kt/n) + n(n-1)(kt/n)2/2! + n(n-1)(n-2)(kt/n)3/3! +….
Something really interesting happens when you let kt=1 in (1+kt/n)n. Don’t worry about why yet. Let us just see what happens.
(1+1/n)n = 1 + n(1/n) + n(n-1)(1/n)2/2! + n(n-1)(n-2)(1/n)3/3! +…
Now lets go a step further. Lets do this binomial series where n is huge! Let n approach infinity. It is called taking a limit. So in each term of the expansion, if n is huge, it is so much bigger than 1, 2, 3, 4, etc., in those expressions like (n-2), we can just replace each of those factors (n-1), (n-2), (n-3), …. by just n. For example, if n is big enough, even for n - 2,000,000, n will be so big, maybe like 200,000,000,000,000, that 2,000,000,000,000,000 - 200,000,000 = 199,998,000,000,000. So to 5 significant figures this rounds to 200,000,000,000,000. So imagine making n really huge, approaching infinity,
The limit of (1+1/n)n as n approaches infinity becomes,
(1+1/n)n = 1 + n(1/n) + n(n)(1/n)2/2! + n(n)(n)(1/n)3/3! + n(n)(n)(n)(1/n)4/4! + …
(1+1/n)n = 1 + n/n+ (n2/n2)/2! + (n3)/n3)/3! + (n4)/n4)/3! + …
And in each term, the the n values are the same in the numerator as denominator, so they cancel out.
Or that limit as n approaches infinity give us
(1+1/n)n = 1 + 1 + 1/2! + 1/3! + 1/4! + 1/5! +……
Which is written like this, and has these values,
The limit as n→∞
(1+1/n)n = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + 1/720+ 1/5640 + 1/45120 +……
Now use a calculator to compute these number. You will get an interesting total.
1.00000
1.00000
0.50000
0.16667
0.04167
0.00833
0.00139
0.00020
0.00002
2.71828
And if we used more terms in the series we could get additional figures. What is really interesting is if you let kt = 2 and go through the same series and calculations. We get (2.71828)2. And if we do it again with kt = 3 we get (2.71828)3. And if we keep repeating and repeating all of those calculations, we always get a numerical exponent equal to kt. (we used kt=1, kt=2, kt=3,…).
Thus, we can no write our equation
N/N0=(1+kt/n)n ,
as n approaches infinity as
N/N0 = (2.71828..)kt
Or as
N = N0 (2.71828..)kt
This is called an exponential function. And this strange base for the exponent is a base that occurs for many situations like the infections. It is a transcendental number we call e
N = N0ekt
If in our situation of infections, we need to know the value of the constant, k.
Suppose that by tracking the infections and keeping a count, we know that the present infection rate is doubling every 2 days. So
N/N0 = 2 = (2.71828)2k
Lets find k by trial and error. If 2k is made equal to 1, we get 2.71828 on the right and that is too big. If 2k is made equal to 1/2 that is a square root, and we find the square root of 2.71828, 1.6487 is too small. So lets try 2k=.75, that is the 3/4 root of 2.7128 is 2.1170. We are getting closer. Lets try 2k=.7 as the root. Then we get 2.0138 and that is really close to 2. Now lets try 2k=.69. We get 1.9937, really close to 2. So try 2k=.693, and we get 1.9997. Finally lets try 2k=.6931. We then get 2.0000 and that is good enough for me.
So we know that 2k=.6931 makes the number of infections double. So k=.6931/2 = .3466.
And we can write an equation for this infection that is doubling every 2 days,
N/N0 = e0.3466t
We do not want to have to use trial and error if we need to make a new calculation where the doubling time changes, and in other applications, like bacterial growth, we have the same problem.
So in mathematics we create a new definition of an exponent. We call an exponent a logarithm. A logarithm must have a base, as an exponent it has a base e. So this is called a natural logarithm, and has a base of e. Our equation can then be written,
Loge(N/N0) = kt
And for a doubling of infections, Loge2 =ktdoubling
And we can find k from
k = Loge2/tdoubling and the doubling time is given by
tdoubling = Loge2/k
Mathematicians use base e exponents to make calculations like we have made by trial and error and have put them into tables in books. They are called Tables of Logarithms. Your calculator also has a function button for natural logarithms. It also has a button for logarithms to the base 10.
Guess what? Remember all of those trials and errors to get .6931? Well, the tables and my calculator shows Loge2 = 0.6931.
Now we can really do things easily.
Suppose that the doubling time for infections is now 5 days. We would have Loge2 = 5k, so that 0.6931 = 5k, and k = 0.1386, and the equation for infections would be
Loge(N/N0) = 0.1386t
Which can be written
LogeN = LogeN0 + 0.1386t
Or
In exponential form,
N/N0 = e0.1386t
If 1,000 people are now infected, how many people will be infected in 30 days?
N/1,000 = e(0.1386)30 = e4.158
Looking up the value of this exponential on the calculator or in tables, we get
N/1,000 = 63.94, or N = 63,940 people.
So starting with 1,000 infected people infecting others, with a doubling time of 5 days, there will be 63,940 people infected within 30 days.
What if we want to know how long it will take for a certain number N of people to become infected? Start with 1,000 infected people and 5 days doubling time. We can use the equation,
Loge(N/N0) = 0.1386t
Dividing both sides by 0.1368
(Loge(N/N0))/0.1386 = tN
Or
7.215Loge(N/N0) = tN
So how long before the 1,000 infected becomes 200,000 infected?
tN = 7.215Loge(200000/1000)
tN = 7.215Loge(200)
And we look up the logarithm to base e of 200 in tables or on calculator.
tN = (7.215)(5.2983)=38.2 days
In general, we can now write the infection growth equation as
Loge(N/N0) = kt
Just like with exponents (since logarithms ARE exponents),
Loge(N/N0) = LogeN - LogeN0
so that Loge(N/N0) = kt, and LogeN - LogeN0 = kt
Which can be written,
LogeN = kt + LogeN0
Suppose you have a table of infections N and for various time t in days. Think about LogeN as a quantity y and think about LogeN0 as fixed value, which it is, and call it b. Think of k as m and t as x.
Then we would have an equation
y = mx + b
You remember that this is the equation of a straight line with slope m and y intercept b.
So if you calculate the logarithm to the base e of each value of N in the table, and then plot a graph of those logarithms versus time in days, the exponential function is going to be a straight line with the slope of that graph equal to the constant k. And the doubling time for the infection spread is going to be just
tdoubling = Loge2/k = tdoubling = Loge2/slope of logarithm base e graph
Lets take a real example, the actual deaths in the United States from COVID-19 for the past 33 days.
These are the data:
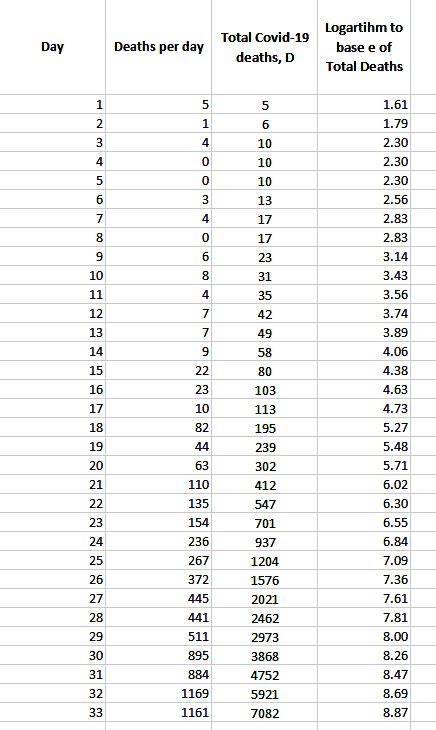
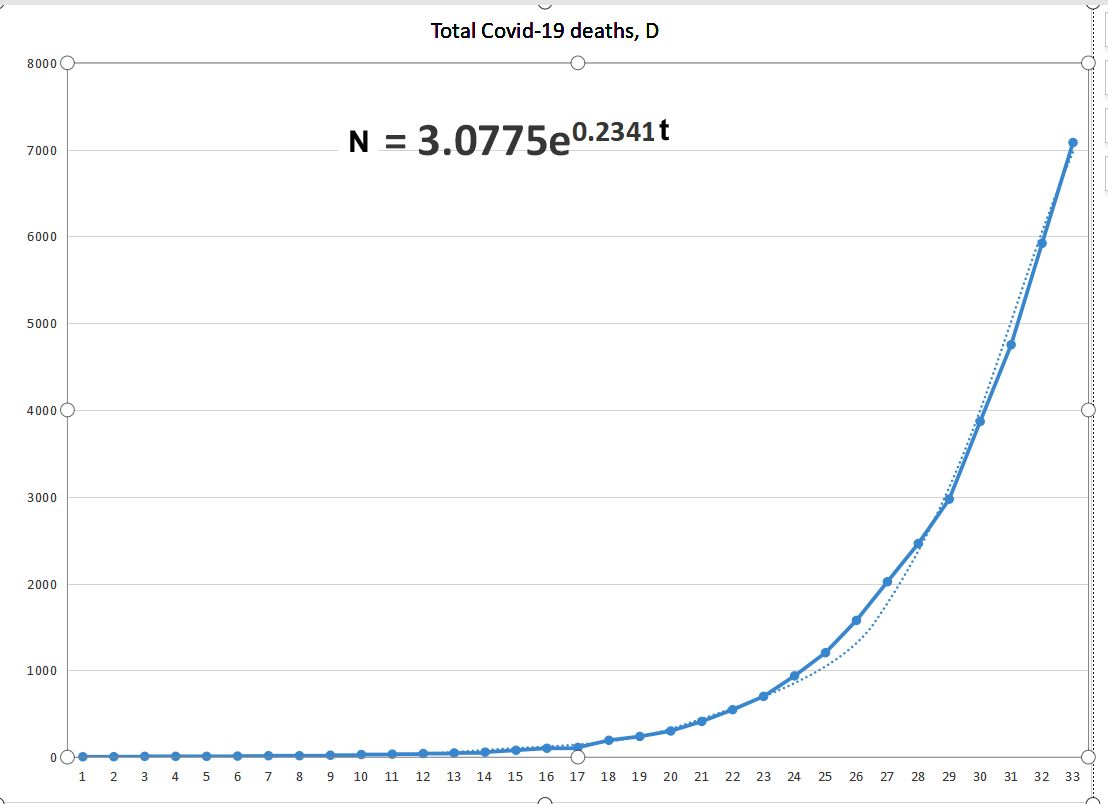
And look at a graph of the deaths, with an exponential trend line matching the graph:
Now look at the graph of the Logarithm of the deaths:
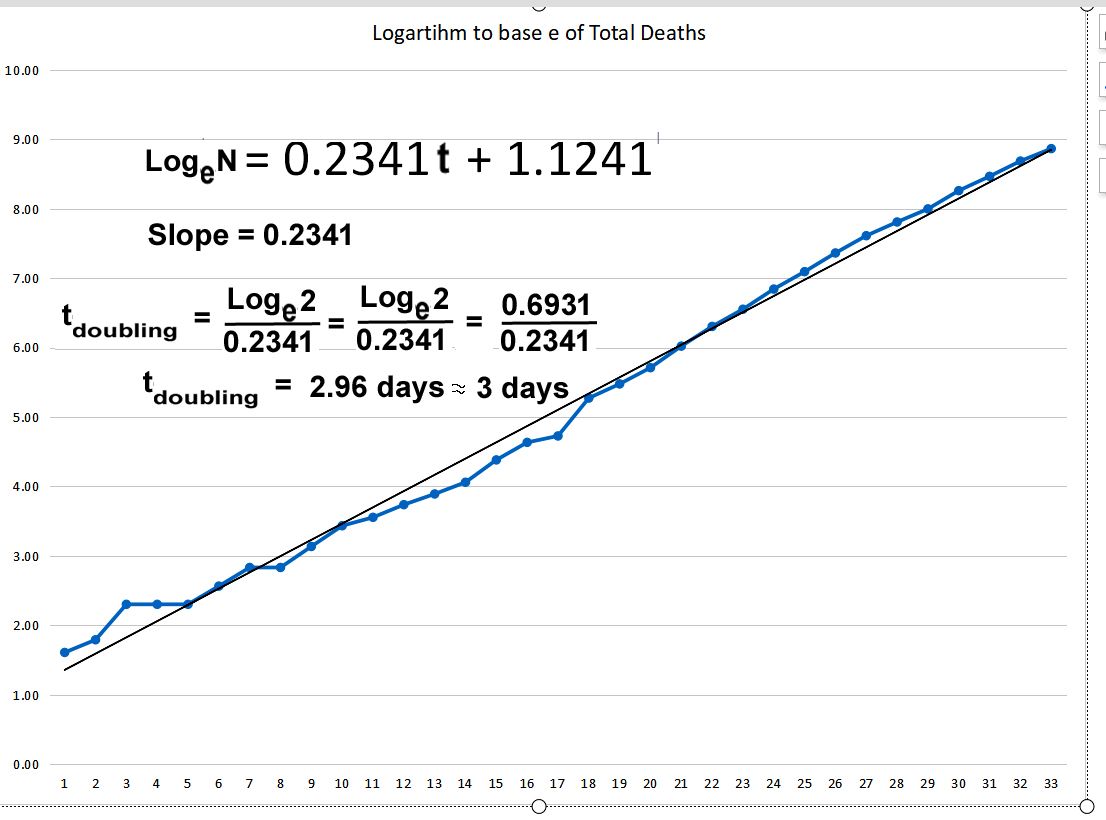
The number of deaths is doubling in the United States every 3 days.
So this is very scary. However, there are always limiting factors. Suppose for example the population has only 100,000 people. Or suppose the virus no longer spreads at the same rate. In such models as this the real world must exactly match all assumptions. And that seldom if ever happens.
This kind of explanation, leading to the spread of a virus applies to many other phenomena: bacterial growth; radioactive decay; discharge of a capacitor; entropy in statistical thermodynamics. And more. All would lead to an exponential with e as the base.