How Good Is Our Sight?

What can we "make out?"

Look at the photo of the flowers.

Now look at just one blossom.

You can see five petals.

Back up and look

Back away from the image of the blossom, as far as you can in the room or where ever you are. Can you still see the individual petals?

But what if I make the photo image much smaller?

At the distance you read a book, you can still see all five petals as individual petals. But start moving backward away from the image. What happens as you get 5 or 10 feet away from it? How about 20 feet away? Why is this?

So if you are looking at a distant tree, can you "make out" individual leaves? Why not?

Another Example.

Look at these two sets of lines, one set of red, and the other a set of blue.

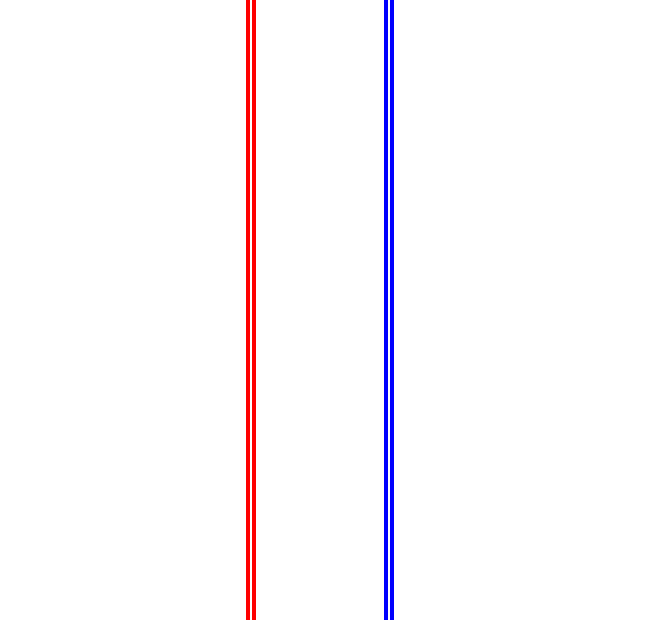
The space between the red lines is the same as the space between the blue lines, and the lines have the same width.

Step back away from the image, and keep moving back until you can no longer see two distinct red lines. At that instant, what about the blue lines? Try looking with the left eye closed and right eye opened; then try it with the right eye closed and the left eye opened.

You will continue to be able to distinguish two blue lines at a distance where you no longer can distinguish two red lines. Why are they different?
Now do the same for violet next to red and next to blue.

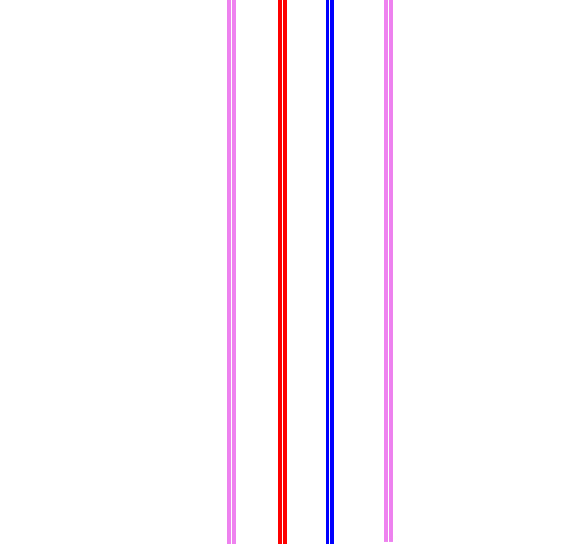
Lets Find the Answers

So why can you not distiguish images of two things at a distance? And why does the color make a difference on which you can see best?

Consider the dimensions of a human eye.

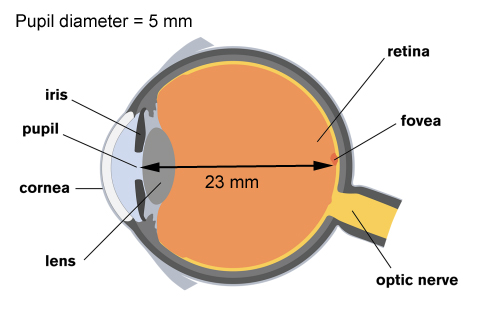
Light enters your eye through the pupil. The pupil is small when there is lots of light, as small as 2 mm, but gets large when there is very little light, as large as 8 mm. For average lighting conditions, the pupil has a diameter of about 5 mm.

When "white light" from a point source passes through a circular hole, and is displayed on a screen, this what you will see.

There is a bright central spot, surrounded by alternating of brightness and darkness. This is called diffraction.

Here is what it looks like when the light is from two closely spaced sources. As the sources are spaced closer and closer together, the diffraction causes the two images to blug together. When that happens you cannot distinguish one source from the other.

One can examine the diffracton of two sources of light and develop an equation that tells under what conditions the two sources cannot be resolved.

For the human eye, having an average pupil diameter of 5 mm, the minimum angle would be given by the equation,

Minimum angle = (1.22/5 mm)x wavelength of light

The average wavelength of "white light" is 500 nm, or in mm, 0.0005 mm. Then the minimum angle must be

Minimum angle = (1.22/5 mm)x0.0005 mm = 0.000122 radians.

Blue light has a wavelength of 470 nm, and red light has a wavelength of 680 nm. So for blue light, this minimum angle will be smaller, about 0.000115. For red, it will be larger, about 0.000166.

So what is a "radian"?
For our purposes, when two sources are close together, the angle in radians is simply the separation of the light sources divided by the distance from the eye to the light sources.

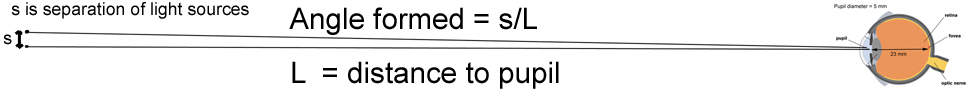
If we make this angle in radians equal to the minimum angle for resolution of two light sources, we have simply,

s/L = 0.000122 for white light, 0.000115 for blue light, and 000166 for red light.

The two parallel lines in the images shown earlier were 0.7 mm apart. So for those lines, we would have L = 0.7 mm/000115 for blue light. This would be 6,087 mm, or about 6.09 meters or about 20 feet. For red light, it would be 4,217 mm, or about 4.2 meters, or about 14 feet.

So if you have excellent eyes, you will see distinct red lines out to about 14 feet, but after that they will appear to be merged into one line.
You will see the blue lines as distinct out to about 20 feet, after which they will appear to be merged into one line.

I leave you with a problem.

Two leaves on a tree are separated by 1 inch. The leaves are green and have a wavelength of 555 nm. How close must you be to the leaves to see them as distinct?
What if it is Fall, and the leaves have turned to a deep red, of wavelength 700 nm. How close must you be?